La "lontananza logica" è definita su misure di similarità/dissimilarità tra le unità
statistiche prese in considerazione. Per dati quantitativi (numerici) possiamo utilizzare
delle misure di distanza, ovvero delle metriche.
Per dati di tipo qualitativo bisogna utilizzare misure matching-type, cioè di associazione (similarità o
dissimilarità). Il punto di partenza è ovviamente la matrice dei dati.
Il raggruppamento dei dati avviene mediante un preciso criterio, suddiviso mediante determinate variabili a seconda della scelta effettuata.
Questo, tra le altre cose, serve per pervenire a sistemi di classificazione automatica o ricerca di classi omogenee.
DENDOGRAMMA
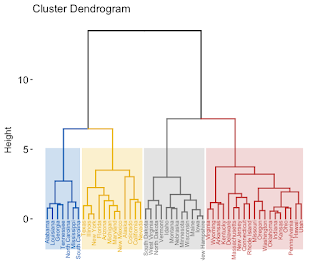
I metodi gerarchici (Johnson, 1967; Everitt 1979) non riguardano una singola partizione delle n unità, ma una serie di partizioni che possono essere rappresentate graficamente attraverso un "dendogramma" o "diagramma ad albero" nel quale sull'asse delle ordinate viene riportato il livello di distanza, mentre sull'asse delle ascisse vengono riportate le singole unità. Ogni ramo (linea verticale) corrisponde ad un grappolo. La linea di congiunzione (orizzontale) di due o più rami individua il livello di distanza al quale i grappoli si uniscono. I metodi gerarchici si distinguono per il modo in cui, dopo la p-esima fusione, vengono calcolate le distanze tra il nuovo grappolo ed i rimanenti.
In poche parole, importati i dati (ad esempio quelli di Excel in un software di cluster analysis) l'algoritmo riunirà i cluster vicini tra loro.
Nel dendogramma di sopra si può notare come Puglia, Calabria, Basilicata e Campania facciano parte di un unico cluster (dati simili tra di loro, per qualche motivo. Poi dipende dallo studio che state facendo).
Il cluster più dissimile da questo si trova nella zona opposta del diagramma: Lazio e Molise ad esempio.
E così via.
ALGORITMI GERARCHICI
Gli algoritmi gerarchici proposti in letteratura (metodo del legame singolo, metodo del legame completo, metodo del legame medio, metodo del centroide, metodo di Ward) si differenziano unicamente per il diverso criterio che regola la valutazione delle distanze tra i gruppi ai fini delle aggregazioni in serie.Nel metodo del legame singolo, la distanza tra i gruppi è posta pari alla più piccola delle distanze istituibili a due a due tra tutti gli elementi dei due gruppi.
L'adozione di questo algoritmo per la composizione dei gruppi evidenzia in maniera netta tutte le similitudini e somiglianze tra gli elementi: privilegia la differenza tra i gruppi piuttosto che l'omogeneità degli elementi di ogni gruppo.
Nel metodo del legame completo, si considera la maggiore delle distanze istituibili a due a due tra tutti gli elementi dei due gruppi.
Questo algoritmo di aggregazione evidenzia in maniera netta le differenze tra elementi: privilegia l'omogeneità tra gli elementi del gruppo a scapito della differenziazione netta tra gruppi.
Avremo rami molto più lunghi, i gruppi (e soprattutto i rami) si formano a distanze maggiori.
Metodo del legame medio rappresenta il valore medio aritmetico di tutte le distanze tra gli elementi.
L'adozione di questo algoritmo per la composizione dei gruppi semplifica notevolmente la composizione dell'albero costruito con l'algoritmo completo, mente rispetto a quello costruito sull'algoritmo singolo rappresenta una movimentazione e differenziazione. Essendo basato sulla media delle distanze, i risultati sono più attendibili e i gruppi risultano più omogenei e ben differenziati tra di loro.
Nel metodo del centroide, vanno determinati i vettori contenenti i valori medi delle p variabili in tutti gruppi (centroidi), e le distanze tra i gruppi viene assunta pari alla distanza tra i rispettivi centroidi.
Infine il metodo di Ward differisce in parte dai precedenti, in quanto suggerisce di riunire, ad ogni tappa del processo, i due gruppi dalla cui fusione deriva il minimo incremento possibile della devianza "entro".
SOFTWARE PAST3
Past3 è un software freeware, nato per la Paleontologia (scienza che studia i fossili e le sue associazioni) ma che ha trovato largo impiego di sviluppo anche in altri campi perchè ovviamente il software "non sa" che tipo di dati stiamo trattando.
Come avrete capito, le associazioni vengono fatte usando criteri di similitudine, una volta scelto l'algoritmo.
Per scaricarlo: Past3 (Download)
Per prima cosa importiamo la matrice di dati (o comunque il foglio Excel dei dati da raggruppare): file/open/scegliamo la cartella e poi il file Excel (ad esempio).
Nella successiva schermata (se settati su names/data entrambi) facciamo ok.
Poi select all.
Edit/rearrange/traspose/select all (ciò serve per settare il giusto ordine dei dati).
Importati i dati, per svolgere l'analisi, facciamo: multivariate/clustering/classical.
Noteremo l'indice di similarità che appunto evidenzia le similitudini dei dati inseriti).
Avremo due modalità di rappresentazione dei dati:
1) Q-Mode (inerente le variabili)
2) R-Mode (sui campioni)
Per saperne di più: Q-mode versus R-mode principal component analysis for linear discriminant analysis (LDA)
RAPPRESENTAZIONE STATISTICA MEDIANTE NUMERI E GRAFICI
Per meglio rappresentare i dati possiamo servirci di altre modalità di visualizzazione: numeriche e grafiche.
Importiamo il nostro foglio Excel, dopodichè facciamo select all/diversity/diversity indices/ok.
Questa è una visualizzazione numerica.
Per quella grafica schiacciate su plot. A destra possiamo evidenziale l'indice voluto (Menhinick, Simpson 1-D, Shannon H, etc).
E' evidenziata anche una barra degli errori che è possibile eliminare togliendo la spunta, in alto a destra.
Per prima cosa importiamo la matrice di dati (o comunque il foglio Excel dei dati da raggruppare): file/open/scegliamo la cartella e poi il file Excel (ad esempio).
Nella successiva schermata (se settati su names/data entrambi) facciamo ok.
Poi select all.
Edit/rearrange/traspose/select all (ciò serve per settare il giusto ordine dei dati).
Importati i dati, per svolgere l'analisi, facciamo: multivariate/clustering/classical.
Noteremo l'indice di similarità che appunto evidenzia le similitudini dei dati inseriti).
Avremo due modalità di rappresentazione dei dati:
1) Q-Mode (inerente le variabili)
2) R-Mode (sui campioni)
Per saperne di più: Q-mode versus R-mode principal component analysis for linear discriminant analysis (LDA)
RAPPRESENTAZIONE STATISTICA MEDIANTE NUMERI E GRAFICI
Per meglio rappresentare i dati possiamo servirci di altre modalità di visualizzazione: numeriche e grafiche.
Importiamo il nostro foglio Excel, dopodichè facciamo select all/diversity/diversity indices/ok.
Questa è una visualizzazione numerica.
Per quella grafica schiacciate su plot. A destra possiamo evidenziale l'indice voluto (Menhinick, Simpson 1-D, Shannon H, etc).
E' evidenziata anche una barra degli errori che è possibile eliminare togliendo la spunta, in alto a destra.




Nessun commento:
Posta un commento